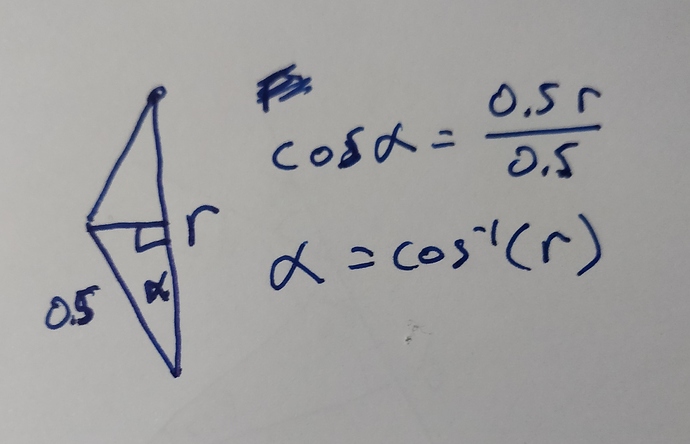"Sandtrails" - a polar sand table

ZenXY Your Builds
61

I couldn’t wait. This is just too interesting.

First, I am going to again push for using the theta rho output. Just because it has a lot of the same challenges and I’ve solved them in sandfy. 1) I use a ton of vertices to create lines, so you won’t have to. 2) I am keeping track of movements around the circle, and I am outputting the angle in a continuous angle. So when a line goes from quadrant 4 to 1, the angle is greater than 2pi. 3) It makes the math much simpler.

I’m going to explain the math. Then I will make a quick program to do the conversion (It will be a fun challenge). Then, we can talk about what other challenges remain.

Math

Sorry for the chicken scratches, I am writing this out on paper.

Theta Rho

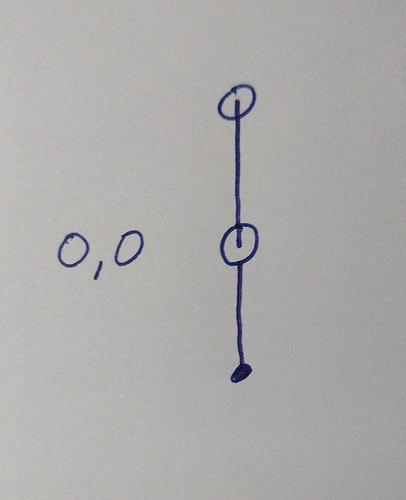
Theta, Rho is the sisyphus format. It is an angle and a radius.

The radius is always between zero and one. So even though you have 200mm radius, the max rho is 1.0.

Theta is the angle, and it always is continuous. It is in radians, and can be positive or negative. This is a simple pattern that would clear the table with 100 turns:

0,0
200*pi, 1.0

0,0

IMG_20200620_224248
IMG_20200620_2242482007×2469 808 KB

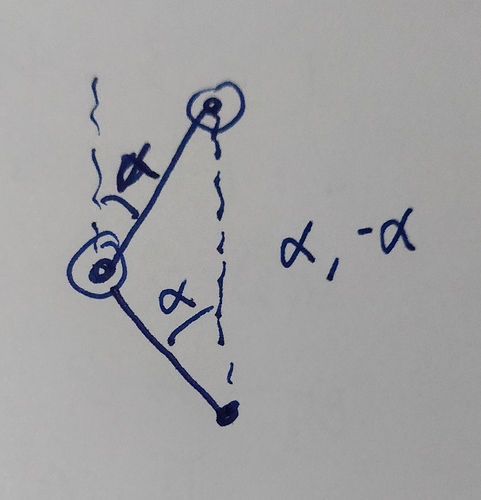
Let’s make zero on your motors straight ahead. Let’s also make this 0,1 in theta rho. Each of your arms are 0.5r long.

Rho

Let’s always assume your arm can only bend one way. It is really neat that it goes both ways, but it isn’t important which way, and we might as well make it easy on ourselves.

If we want to keep theta at 0, but make r something else, we can do this:

IMG_20200620_224253
IMG_20200620_2242531740×1808 390 KB

When we do that, the first motor is at alpha and the second is at -alpha. We’ll calculate alpha in a minute.

Theta

So, if we add an angle to both motors, we will move theta, but not Rho.

IMG_20200620_224307
IMG_20200620_2243071713×1637 370 KB

So we have:

Motor1 = theta + alpha
Motor2 = theta - alpha

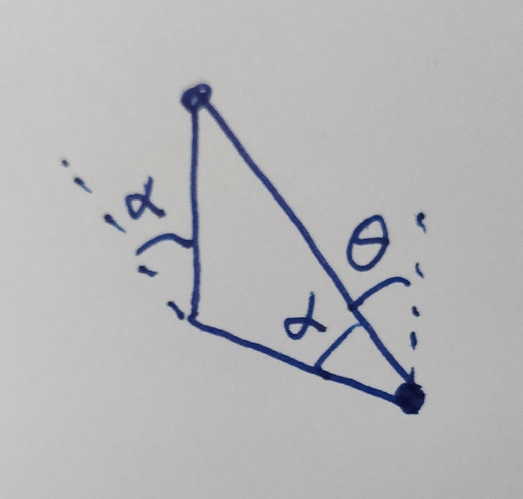
Alpha

Going back to the triangle when we first saw alpha, we can split it into two right triangles. In the closer triangle, the hypotenuse is 100mm, but we know that is 0.5 in our normalized size. The height is half of Rho, so we have:

IMG_20200620_224259
IMG_20200620_2242592660×1715 371 KB 

cos(alpha) = 0.5 * r / 0.5 = r
alpha = cos^-1(r)

Motor Output

Motor one (in the middle) I’ll call M1. Motor two (on the arm) is M2:

M1 = theta + cos^-1(rho)
M2 = theta - cos^-1(rho)

Those are in radians. So to get gcode X, Y, we need to multiply by 6.0/(2pi).

Code

Sorry, I don’t know visual basic well, and I run linux, so I don’t think there’s a good way for me to run it. I took a stab at implementing this in python though. I went ahead and used an online editor, so you can go there and try it, without needing python on your machine.

repl.it code

import math

# Config
MOTOR_1_UNITS_PER_ROTATION = 6.0
MOTOR_2_UNITS_PER_ROTATION = 6.0
INPUT_NAME = 'sandify.thr'
OUTPUT_NAME = 'transformed.gcode'

# Open the files.
with open(INPUT_NAME, 'r') as infile:
  with open(OUTPUT_NAME, 'w') as outfile:

    for line in infile:

      # First, separate by content and comments
      parts = line.strip().split('#')

      if len(parts[0].strip()) == 0:
        # This line doesn't have anything that isn't a comment
        outfile.write(line.replace('#',';'))
        continue

      else:
        (theta, rho) = parts[0].split()

        # Here, we're actually doing the math.
        m1 = float(theta) + math.acos(float(rho))
        m2 = float(theta) - math.acos(float(rho))

        x = MOTOR_1_UNITS_PER_ROTATION * m1 / (2*math.pi)
        y = MOTOR_2_UNITS_PER_ROTATION * m2 / (2*math.pi)

        outfile.write("G1 X{:0.03f} Y{:0.03f}\n".format(x, y))          

    # We just moved each motor a bunch. A whole lot.
    # When we start the next file, we don't want it to unroll
    # So we will make the current coordinate something that is small, but the same.
    xmod = x % MOTOR_1_UNITS_PER_ROTATION
    ymod = y % MOTOR_2_UNITS_PER_ROTATION

    outfile.write("G92 X{:0.03f} Y{:0.03f} ; Reset the coordinates\n".format(xmod, ymod))

In that repl website, you can upload a sandify.thr file, and hit run. It will write out the transformed.gcode file, which you can inspect and down.

Running it.

Do you have endstops? You’ll want to make sure the machine starts upright with both arms fully extended, and set to X0 Y0.

At the end, it will have X,Y values out in the hundreds or thousands. When you start the next one, you don’t want to have to reset it, and you don’t want to have to unwind the whole thing. So I added a G92 at the end of the file. You will want to make sure you do things like select the always end on perimeter function in sandfy and then maybe add a G1 X0 Y0 to the end of the file to bring it around to the top again.

If you have resolution problems, you can reduce the steps/mm in Marlin, and increase the config constants in the script. at 6000 segments/revolution, we have a resolution right now of 0.06degrees. That seems about right to me.

This is the pattern I made to test it out:

sandify

transformed.gcode (34.8 KB)

More Thoughts

This was really interesting and I couldn’t stop thinking about it. Thank you for sharing it. I hope all of this is clear, and I obviously didn’t try it on a machine, so I hope got it close to right. I was shooting for clarity, but I can sometimes lean into condescending. This is a tricky problem, I know. I hope I didn’t completely miss the mark.

3 Likes