Which part of the puzzle am I missing? You say you’ve measured 6Ohms with all the connectors and wires, but at 1A limits and 12V supply, you’re going to be at 50% duty cycle. Why does it matter if you can get to 1A with 25% duty cycle?
It seems a bit like driving faster towards a stop light.
I’m quite sure I’m just not thinking of some part, but my napkin math just doesn’t add up.
Why does it matter if you can get to 1A with 25% duty cycle?The controller has no trouble keeping the winding current at the setpoint when the motor is at rest, assuming the total resistance allows at least a few volts of headroom at the setpoint current.
When the motor is turning, however, back EMF further reduces the voltage available to change the winding current. As the speed increases, the reduced supply voltage means the current can’t change fast enough to produce the expected torque during each (micro)step and, at some speed, the motor stalls.
For example, the long current ramp during the second (micro)step limits the available torque to maybe 3/4 of the expected value:
At twice the speed, back EMF further reduces the available voltage, so the current couldn’t reach the commanded value during the half-as-long (micro)step. The next step requires even more current, so the winding current falls further behind the setpoint level until the motor stalls.
A higher power supply voltage gives the controller more headroom against wiring resistance and back EMF. As long as you keep the motor speed low enough, there’s no problem with a 12 V supply, but it limits the available torque at even moderate speeds.
More voltage → faster current change → more torque at speed → better performance → happier user!
Thanks for the thoughtful explanation. You don’t have to spend time educating a complete stranger on the interwebs, and it’s appreciated. I saw that graph in your last link, and maybe I’m making a mistake understanding what you’re trying to illustrate.
I assume the PWM on the bottom represents the step signal, so on a rising edge, it’s trying to go to the next microstep. I am also assuming the other line, with the dramatic slope is the current. It looks like the width of the PWM is 200us? I’m not sure what the amplitude of the slope is, but in your description you mention 220mA and 1/8th microstepping (if it was 1/1, then it would try to get all the way to 1A, but have 8x time to do it).
When the current graph climbs, the slope is higher in the 18V case, which is what you’re trying to point out, I think. But when it stops rising, and goes into the saw tooth pattern, that’s the driver already reaching it’s set point. So in both these graphs it’s made it to the set point before the next step. Right?
So the argument is that if the step times are smaller than the amount of time of the first climb, then it wouldn’t reach full current before the next step. The 9V graph is about 135us, or 7400ish steps/s. This is the microstep, but I would guess that the finer the steps, the smaller the current needs to go each step, so it’s probably close to a wash. You also said 1/8 microstepping (which seems about right for 200mA on the first jump). At 1/8 microstepping, that’s 50steps/mm(MPCNC), so 7400steps/s / 50steps/mm = 148mm/s max at 9V. Any faster than that and you won’t get full current.
Getting to the set point earlier than the next step doesn’t make anyone happier, except electronics manufacturers. :). (Glib comment aside, thanks again for talking through this with me, seriously).
OR, is the point that the total torque is proportional to the area under the current graph, and so there is more power if it climbs faster?
The general idea goes like this:
Motor torque is proportional to winding current, as is the IR loss due to wire resistance, while back EMF is proportional to rotational speed. The voltage available to drive the winding current is thus the power supply voltage reduced by the IR loss and back EMF.
The steppers have 200 full steps per revolution, with the controller dividing each full step into microsteps, typically 16 or 32, for a total of 3200 or 6400 microsteps/rev. Each microstep has a specific relation between the two winding currents, defined as the sine and cosine of an angle running from 0° to 360° every four full steps.
The vector sum (RMS value) of the two currents adds up to the nominal winding current set by the twiddlepot on the driver board. For example, a 1 A setpoint will produce 0.71 A current in both windings during the 45°, 135°, 225°, and 315° microsteps. Anything that changes the relationship between the two winding currents will affect the direction of the force applied to the rotor and disturb its rotation.
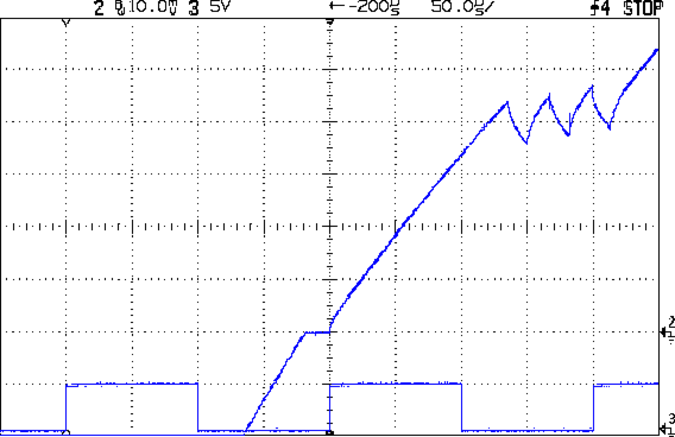
The controller must change the winding currents at the start of each microstep, then stabilize the currents at their new values, by applying the power supply voltage to the ends of the wires leading to the motor. Because the motor winding inductance limits the current’s rate-of-change, the controller uses PWM to switch the voltage much faster than the winding’s time constant to make the average current closely track the desired setpoint. That’s the sawtooth part of the waveform, over on the right side:
Here’s how it all fits together.
The long rising slope in the middle of the screen shows this equation in action:
V = L Δi/Δt
Where L = winding inductance and Δi/Δt = current rate-of-change.
The effective voltage V at the winding is the supply voltage reduced by the IR loss and the back EMF. You can’t measure the effective voltage directly, but it pops out of the equation when you know the inductance (from the motor datasheet) and measure the Δi/Δt from the rising slope. The linkie above the picture has the calculations for a different motor & supply voltage.
So the power supply voltage, current setpoint, and back EMF determine Δi/Δt. The current setpoint comes from the motor datasheet (it’s a “1.0 A” or “1.5 A” or “2 A” motor), so you know the IR loss in the wires. The back EMF comes from the motor speed, which you pick to be faster than anybody else’s MPCNC [grin].
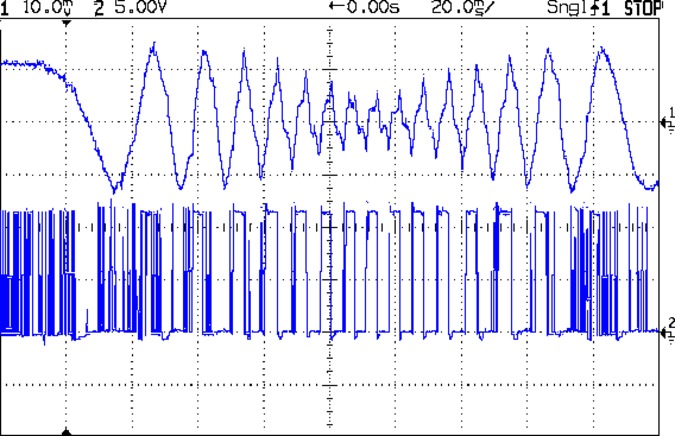
As long as the speed remains low enough, the controller can change and regulate the winding currents during each step. When the speed gets too high, the controller loses control and produces the wreckage in the middle of this trace:
The bottom trace shows the controller’s PWM switching, which should always be similar to the narrow spikes over on the left. In the middle, where the motor reaches 60 mm/s, the “PWM” degenerates into wide pulses as the increasing back EMF reduces the available voltage, the Δi/Δt falls, and the current can’t reach the proper value during each microstep. Because the current doesn’t reach the setpoint (the peak values as the motor starts and stops), the torque drops and the motor tends to stall in the middle of the move.
I picked absurdly high speeds to show the effects for the Circuit Cellar column, but when folks kvetch about “missed steps” and suchlike, you’re seeing the equation in real life. If the motor speed remains low enough, then a low power supply voltage works just fine.
However, the power supply voltage provides the only knob available when you feel The Need For Speed or the need for more torque at a given speed. In round numbers, going from 12 V to 24 V adds enough headroom to make 133 mm/s = 8000 mm/min traverse speeds possible, if not practical.
I did an analysis of the crappy stepper motors Makerbot used in the original Thing-O-Matic, back in the day, with truly grisly detail. It’s more than you really want to know, but provides more info on most of the topics. The comments were enlightening, too.
(Ryan: This may be a dupe, but might be better worded than my earlier attempts)
SO where is the speed limit? It looks like if the slope is longer than the step period, you get the wreckage in your graph. There’s probably a reduction of power approaching that, but getting to the sawtooth phase is enough to reach the desired current (if only for a moment).
My current mental model is that with higher voltage, the slope will rise faster, and the area under the curve will be larger, so you’ll get some drop in total current for the step with lower voltages. At some point, the slope won’t be enough to reach the set point in time, and it will then dramatically lose current, torque, and power, right? So what speed is that drop off? The first graphs, with the comparison between 9V and 18V slopes led me to think that was at 148mm/s (did I do that math right?). The wreckage graph is only at 60mm/s (which is still at 100 16ths steps/mm). It’s important to know about where it is, because a significant drop in torque at 40mm/s is enough for me to look into 24V. A drop at 150mm/s doesn’t matter to me at all.
Usually, when I skip steps, I’m moving at 10mm/s, and milling, but I haven’t tried to max out my rapids either.
How much of that waveform is dependent on actual physical motion of the stepper? Isn’t there a lag due to physical inertia/resistance/friction involved in here somewhere and how much does actual stepper ability to follow the changing magnetic field affect the magnetic field?
So Ed talks about the back EMF being proportional to speed. The other side of the problem is that when the stepper hits resistance, the amount of torque is either enough to move the motor shaft forward enough to the next step, or it’s not, and the external torque will win and send the motor shaft back to the previous step. In that sense, the fact that the sine wave in the wrecked graph has lower peaks means that there’s smaller torque getting to the shaft, and the smaller the external torque needs to be to overcome the motor torque and make it miss a step.
a lag due to physical inertia/resistance/frictionOn the scale of the PWM pulses, the motor speed (and, thus, back EMF) is pretty much constant, so you can make a bunch of simplifying assumptions and not be too far wrong.
getting to the sawtooth phase is enough to reach the desired currentTiming, however, is everything. The motor must have the proper winding currents during essentially all of each microstep in order to produce its rated torque. To the extent the currents aren't correct, the motor doesn't operate properly. To the extent the currents don't reach the proper value, the motor can't generate the proper torque.
So what speed is that drop off?It depends on what you consider to be "isn't operating properly", of course!
Let’s run the numbers for your example:
moving at 10mm/s, and millingSuppose that's along the X axis:
No wonder it stalls!
a significant drop in torque at 40mm/s is enough for me to look into 24VSoooo, it looks like wreckage at 10 mm/s. I'd expect something like the triangles two or three cycles in from the ends, where it's running relatively slowly:
Double the supply voltage to 24 V (modulo the usual caveats about expecting too much from Chinesium) and see what happens. I’d expect a dramatic improvement with no other tweakage.
Caveat: I’ve been wrong doing calculations in real time, so don’t be surprised if a number’s off by a bit (or a lot). The general principle holds, however; run your own numbers and see what pops out.
I’ll be looking carefully at that math, after I spend a minute finding the right gif, I will check that out.
I don’t have a 1.5A, I have a 1A, but the 6x doesn’t seem right. You measured 6Ohms across the wires and everything, and 2.2Ohms is the motor coil, so it should be:
1.0A (or 1.5A, sure) * (6Ohms - 2.2Ohms) = 3.8V (or 5.7 for 1.5A)
amiright?
I’m not sure why there is a 2x in the inductance value. Also, that’s higher than your motors, which are 2.6mH, right?
If I used 1A, 3.8Ohms, and 2x2.4mH, then that ends up with 1625 A/s.
One whole step is from 0 degrees to 90 degrees, right? So it should be 1.5A * sin(2.815)? or just 7.5ma
A whole step would take 160ms, and using the rest of your math, we could achieve 43A/whole step, which is far greater than the required 1.5A, so something seems wrong with the microstepping math. I understand that if it was on the hairy edge that would be the difference between a sine wave and a triangle wave, but 30x seems like plenty of headroom.
Also, I feel like saying that I am really enjoying this, and I understand 30x more than I did a few days ago. Thank you so much for sticking around here.
I did this sine wrong, it’s actually 75 mA, which sounds about right, since 1500mA/32 is 47mA, and the first step would be the biggest.
Remember: the motors are in series, so you have twice the resistance and inductance for one motor, plus resistance in the harness to / between the controller and the motors. I measured 6 Ω end-to-end and the motor datasheet says 4.8 mH/phase, but your setup will surely be different.
The model for each motor winding is a resistor (the winding wire resistance) in series with an inductor (the coily winding), so, for two motors in series, you have three series resistors: one wiring harness and two winding resistances. The voltage available for each inductor is the supply voltage minus the total IR drop in all the resistors, then divided by two to pu half the voltage in each motor. Plenty of simplifying assumptions, but pretty close to reality.
Pondering the stepper controller datasheets (TI DRV8825 and Allegro A4988, modulo the usual warnings concerning knockoffs) will help understand microstepping, because they have prettier pictures & graphs than I can draw. Those scope shots came from a variety of test setups and I’d be unsurprised to discover I used the wrong microstepping count somewhere along the way.
Hey, look, somebody’s wrong on the Internet! [grin]
So, nope. Strike one:
Nope, strike two:
I still think this is right (except it leaves us with 73mA, instead of my original math). One full step is switching current through coil A to coil B, which is 90 degrees of the circle. Here’s 1/4 stepping from the a4988 doc:
[attachment file=88174]
There are 4 steps from 0 to 1, and 4 more from 1 to 0, and 4 more from 0 to -1. You can also see clearly that the first step requires the largest gain/step, since the slope is highest when crossing zero.
For 1/32 stepping, the current change needed is Amax * 0.05
For 1/16 stepping, the current change needed is Amax * 0.10
For 1/8 stepping, the current change needed is Amax * 0.20
For 1/4 stepping, the current change needed is Amax * 0.38
I agree with the rest of the math.
This is really interesting…
I made a spreadsheet with different speeds, going through these numbers. I got the same answer for 10mm/s, but with my edits for microstepping phase.
(I think you can save a copy and edit the stuff on the left to see how things change stuff.)
Interestingly, the dropoff is between 16 and 17mm/s.
For the google adverse:
[attachment file=88178]
I guess the next step for me is to measure or get the numbers from my actual machine, and see if this is close. I wish I had a good way to measure current like in your graphs. I would be pleased as punch to measure the current at 16mm/s and see it just barely make it in time.
Something must go wrong with the model when the back emf is high enough that the voltage for the inductance goes negative? Now I have to run my CNC at 80mm/s and see what happens.
BTW, for any readers who have made it this far, remember that this doesn’t negate any of the work done in the gallery at 12V. There are plenty of examples of peole running these machines at fast travel speeds without skipping steps.
Another question. The voltage drop due to IR is 1.5A * 6Ohms, but when taking the first microstep, it’s actually going from 0A to just 74mA. When it gets closer to 1.5A, the steps are smaller. On the last 1/32nd step it goes from 1.499A to 1.5A. The voltage drop due to internal resistance should be a lot smaller then, right?
Another issue is that if the motors are wired in series (or not, really) then the max current is set to 900mA. It used to be set closer to 1.5A, but that was for parallel motors.
If I plug in 900mA, I get the cutoff moved to 53mm/s.
Looks like I used a 1:8 microstep picture with 1:16 figures; things go downhill from there.
Remember, all of this modeling boils down to rule-of-thumb approximations. The real test is to measure the actual current, which requires somewhat more test gear than can reasonably be expected, to see what’s going on.
If you’re feeling adventurous, you can use one wire of the harness as a current-sensing resistor: measure the wire resistance, connect a scope across the wire, and the waveform will give you the current. For example, a 0.25 Ω wire will give you a 250 mV/A = 4 A/V waveform. Note that the wire has nothing in common with circuit “ground”: connecting the ground clip of a line-operated scope probe to the wire will kill the driver chip stone cold dead.
For back EMF, feed motor speed into the measured values for the motor, then knock that value off the supply voltage; worry about the phase angle between the back EMF and the microstep angle at some point. As the effective voltage goes down, the current goes down, and the motor stalls: the controller can’t produce more back EMF than that.
The IR drop varies with the current, so it’s a minimum when the sine wave crosses zero and maximum at the peaks. However, when you’re looking for trouble, don’t start by minimizing the trouble. You’re not showing why something works, but why it might not; always expect reality to be worse than your assumptions.
Accelerating that huge mass hanging on the gantry requires more torque than cruising along at top speed, which means the acceleration limits influence the results. A sufficiently low acceleration may prevent the motor from reaching top speed during a short move, which will screw up all your calculations.
Basically, you cannot determine a hard speed limit from these simple models. What you can get is a better understanding of how speed, torque, and supply voltage interact, which is nothing to sniff at!
