If you don’t like math, you should stop reading now. ![]()
I’m working on an extension to the FluidNC UI v3 to automate z leveling but this calculation applies more broadly. I think I’m chasing zeroes a bit but could use some help.
The current instructions for figuring out the values are a bit of an educated guess and check, and that is sufficient, but I’m looking to do the math.
a = Difference between Z probe values between the left and right X locations
b = Difference between left and right probe X locations
It’s kinda like b is the spoilboard, c is the gantry-ish, and a is the offset.
You can’t just take a and use that for your offset because you need to consider the full X width, so it’s going to be larger.
So, you can find the hypotenuse c and \angle{A} in radians:
c=\sqrt{a^{2} + b^{2}}
\angle{A}=\arcsin{\frac{a}{c}}
If you then re-calculate the height using \angle{A} for the full width, it should give you the right value.
If you have the full triangle as d/e/f similar to a/b/c, you have:
e = full width
\angle{D}=\angle{A}
f=\frac{e}{\cos{\angle{D}}}
Ultimately, we want to find d.
d=\sqrt{f^{2} - e^{2}}
If I’m correct to this point, my real question is, what is that full width to use in the calculation?
- Lead screw to lead screw? This is my guess but I was overshooting the value a bit.
- XZ plate to XZ plate?
- YZ plate to YZ plate?
- Left bearing to middle of Y rail?
Javascript function for reference:
function getZOffsetChange(xDistance, xTotalDistance, zDistance) {
// Calculate angle
var a = zDistance;
var b = xDistance;
var c = Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2));
var angleARad = Math.asin(a/c);
// Extrapolate over full distance
var angleDRad = angleARad;
var e = xTotalDistance;
var f = e / Math.cos(angleDRad);
var d = Math.sqrt(Math.pow(f, 2) - Math.pow(e, 2));
// Keep 3 decimal places
return +d.toFixed(3);
}
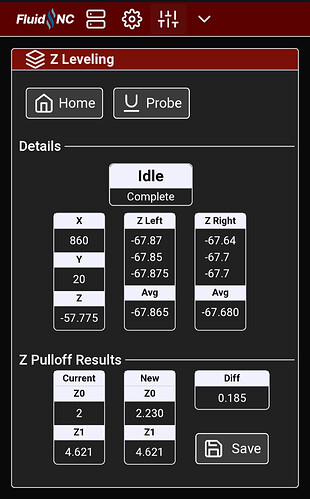
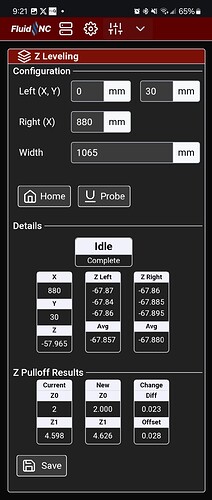
Here’s what my extension looks like at the moment. There are some hardcoded numbers I need to parameterize (860mm between probing values, don’t remember which total width I was using). This was after I ran it the first time and set the values, and then ran it again to see how far off it was. Either way, 0.2mm is tiny.
Functionally, you click the Home button to home all axes. Then click the Probe button, which jogs to a starting X,Y location (currently hardcoded to 0,20 for me), starts the probe, once it returns to idle stores the Z position and jogs Z up, repeats the probing 2 more times, moves to the right position (currently hardcoded to 860,20 for me) and repeats the probing. When it’s done, it calculates the results and you click save to update the values and save. So, you do that all by clicking 3 buttons and holding the touch plate for 6 probes.